引言

SLAM作为机器人和自动驾驶领域的核心问题之一，其目标是在未知环境中实现同时的定位和地图构建。其中在求解多观测约束下的位姿估计问题时，GN和LM算法在求解非线性最小二乘问题方面扮演了重要的角色。为嘛呢？因为这俩思想非常简单实用。博主个人认为，这两种方法的一个共同的优点是快，简单，准确度可以接受。接下来，从一个SLAMer的角度看待GN和LM算法。注意，本篇不涉及代码编程和复杂的理论说明，仅有公式推导，旨在用白话来讨论GN和LM算法。如有逻辑上的不严谨，欢迎各位批评指证。

1. 一个非线性优化问题的建模

一个SLAM问题通常可以被描述为一个最大后验概率问题，也叫MAP（Maximum ）问题，即我们想根据历史时刻已观测到的数据$z$和状态$x$，以及控制量$u$，得到最有可能的下一时刻的状态$x_{t+1}$（因为SLAM的核心本质是Localization嘛），用公式来描述就是

\[x_{t+1} = \underset{x}{argmax} P(x_{t+1}|z_{0:t}, x_{0:t},u_{0:t})\]

这其实是一个很抽象的描述公式，因为我们能通过公式看到SLAM问题的目的是什么，但是我们无法找到一个具体的代入方法和求解方法。并且，求解MAP问题本身是一个比较复杂的问题，求解方法也有很多种，比如粒子滤波，卡尔曼滤波等等。而本章所说的非线性优化，也是求解MAP问题的一个有效的途径。

我们以一个纯激光SLAM为例，激光雷达带来的是一系列的点云，我们可以把每一个点都看作是一次对环境的观测，对一个SLAM（或者是Localization）问题，最重要的是要推算出雷达的当前位置$\mathbf{x}^{L}_{t}$，而且我们还知道在一个3维空间下的刚性变换$\mathbf{T}$可以用旋转矩阵$\mathbf{R}$和平移向量$\mathbf{t}$来表示，那么我们可以将雷达的当前位置表示为

\[\mathbf{x}^{L}_{t} = \prod_{i=0}^{t-1} \mathbf{\bigtriangleup T}_{i} \cdot \mathbf{x}^{L}_{0}\]

用大白话讲，雷达当前的位置相当于对雷达初始位置$\mathbf{x}^{L}_{0}$逐步进行变换$\mathbf{\bigtriangleup T}_{i}$即可，那么我们的问题就转换为如何求取$\mathbf{\bigtriangleup T}_{i}$。

现在我们假设，经过一个刚性变换$\mathbf{T}$的前后两帧雷达点云分别为$P_{A}=\{ p^{A}_{i} \}$和$\mathcal{P}_{B}=\{ \mathbf{p}_{j} \}$，并我们在不考虑噪声和异常点（outlier）的前提下，这两坨点云理应满足

\[\begin{matrix} \mathcal{P}_{B}= \mathbf{T}\mathcal{P}_{A} \\\\ \sum ||\mathbf{p}^{B}_{j} - \mathbf{T} \mathbf{p}^{A}_{i}||_{2} = 0\end{matrix}\]

这两个式子意思就是，变换前的雷达帧历经一次刚性变换$\mathbf{T}$后，应该与变换后的点云完全重合（在点的对应关系已知的情况下）。But！这只是一个非常理想的情况，现实情境下，是不可以忽略噪声和异常点的！

OK，那么我们现在将这些因素考虑进去。假设我们给每个点加一个高斯白噪声，即$\mathbf{p}_{i}\sim N(\mathbf{p}_{i}, \mathbf{\Sigma}_{i})$，这里由于一个点可做是一个3维向量，因此每个点服从一个多维高斯分布。也就是每个点的位置分布情况是涉及到一个概率的，我们知道高斯分布有个优雅的性质，多个独立的高斯分布的线性组合依旧是高斯分布，那么我们可以推出

\[(\mathbf{p}^{B}_{j} - \mathbf{T} \mathbf{p}^{A}_{i}) \sim N(\mathbf{d}_{ij}, \mathbf{\Sigma}_{j} + \mathbf{T}^{T} \mathbf{\Sigma}_{i} \mathbf{T})\]

哎！？这个好，这个公式看起来很优雅，这时我们就在想，如果每个点之间都是独立的，这个$**\mathbf{T}$只要能让每个点对的差值$\mathbf{d}_{ij}$为0的联合概率最大**不就完了么！！吆西，那么说做就做，我们得到下面这个式子

\[\begin{align} \mathbf{T} & = \underset{\mathbf{T} }{argmax} \prod P(\mathbf{p}^{B}_{j} - \mathbf{T} \mathbf{p}^{A}_{i})\\ & \overset{log}{=} \underset{\mathbf{T} }{argmin} \sum \mathbf{d}_{ij}^{T}(\mathbf{\Sigma}_{j} + \mathbf{T}^{T} \mathbf{\Sigma}_{i} \mathbf{T})^{-1} \mathbf{d}_{ij}\\ & = {\color{Red} \underset{\mathbf{T} }{argmin} \sum \mathbf{d}_{ij}^{T}(\mathbf{\Sigma}_{ij})^{-1} \mathbf{d}_{ij}} \end{align}\]

解释一下，公式（1）表示的是联合概率最大化，但是求积操作不好算，况且高斯分布里含有指数$exp(\cdot)$，所以在这里两边取对数操作来去掉指数和常数项，化积为和。最终化简出来的公式（3）正式描述了一个非线性最小二乘问题，也是ICP配准问题的核心公式。

现在我们换一个思路来理解上面公式（3）并且将里面的符号转换成一个易于理解的形式。众所周知，最小二乘问题的本质思想是：让真实值与理论值的差距之和（即残差）最小。从这个思路出发，我们可以发现，公式（3）中的$\mathbf{d}_{ij}^{T}\mathbf{d}_{ij}$其实就是最小二乘中的残差项，而$(\mathbf{\Sigma}_{ij})^{-1}$只不过是给每一个残差项成了一个权重系数，因此博主习惯把$(\mathbf{\Sigma}_{ij})^{-1}$称为权重矩阵（当然这个矩阵的名号很多，比如说信息矩阵，马氏距离…）。这个如果点对的协方差越小，代表对位置的信任程度，就越高，自然权重就越大。OK，这样一个针对非线性优化的最小二乘问题就描述完了！下面呢，为了便于理解，我们还是用$\mathbf{e}_{ij}$表示残差，用$\mathbf{\Omega}_{ij}$表示权重矩阵（信息矩阵），即

\[\mathbf{T} = \underset{\mathbf{T} }{argmin} \sum \mathbf{e}_{ij}^{T}\mathbf{\Omega }_{ij} \mathbf{e}_{ij} \quad\ \ \ (LSQ)\]

2. 高斯牛顿优化算法（Gauss-Newton）

我们现在有要解决的目标优化问题，那么该如何求解呢，梯度下降法教会了我们通过迭代求解最小值时，要往梯度（导数）下降最大的方向走，但是如何求梯度呢？这个时候高斯牛顿法对此有了新的方案。

话不多说，我们开始进入正题（原谅博主废话过多），第1章中每一个残差项可以看作是一个关于$\mathbf{p}^{A}$的函数（因为我们是想让通过调整$\mathbf{P}_{A}$来对齐$\mathbf{P}_{B}$），以下简称$\mathbf{e}(\mathbf{p})$。现在我们对$\mathbf{e}(\mathbf{p})$在$\mathbf{p}$附近进行一阶泰勒展开。

\[\mathbf{e}(\mathbf{p}+\Delta\mathbf{p}) = \mathbf{e}(\mathbf{p}) + \mathbf{J} (\mathbf{p})\Delta\mathbf{p} \quad \ \ \ \ (Taylor)\]

这里的$\mathbf{J} (\mathbf{p})=\frac{d \mathbf{e} (\mathbf{p} )}{d\mathbf{p} }$ ，也就是江湖上令人闻风丧胆的雅可比矩阵（Jacobian Matrix），为啥闻风丧胆？且看后续推导，现在我们只需要假设已知$\mathbf{J} (\mathbf{p})$就好啦。

这里需要说明两点：

泰勒的意义是什么，在G-N优化中，我们并不是直接求两坨点云之间的变换$\mathbf{T}$，而是通过迭代求解，每次迭代会寻找一个的增量$\Delta\mathbf{T}$，使得$\sum \mathbf{e}_{k}^{T}(\Delta\mathbf{T}\mathbf{p}_{k})\mathbf{\Omega }_{k} \mathbf{e}_{k}(\Delta\mathbf{T}\mathbf{p}_{k})$尽可能的小

符号的说明，有人就要怼我了，怎么还一会用$\Delta\mathbf{T}\mathbf{p}$，一会用$\mathbf{p}+\Delta\mathbf{p}$。其实这里两个表示方法是同一个意思，都表示为对一个点做一次刚性变换，只不过在推导数学公式时，我们可能更习惯使用求和而已。

这里我们旨在求解每次迭代过程中的最优$\Delta \mathbf{p}$即可，我们将上面泰勒展开式子代入到公式（LSQ）中，并进行推导

\[\begin{align} \bigtriangleup \mathbf{p} & = \underset{\mathbf{\bigtriangleup p} }{argmin} \sum \mathbf{e}_{k}^{T}(\mathbf{p} +\mathbf{\bigtriangleup p} )\mathbf{\Omega }_{k} \mathbf{e}_{k}(\mathbf{p} +\mathbf{\bigtriangleup p}) \\ & = \underset{\mathbf{\bigtriangleup p} }{argmin} \sum [\mathbf{e}_{k}(\mathbf{p}) + \mathbf{J}_{k} (\mathbf{p})\Delta\mathbf{p}]^{T} \mathbf{\Omega }_{k} [\mathbf{e}_{k}(\mathbf{p}) + \mathbf{J}_{k} (\mathbf{p})\Delta\mathbf{p}] \\ & = \underset{\mathbf{\bigtriangleup p} }{argmin} \sum (\mathbf{e}_{k}^{T}\Omega_{k}\mathbf{e}_{k} +\mathbf{e}_{k}^{T}\Omega_{k}\mathbf{J}_{k}\mathbf{\bigtriangleup p} + \mathbf{\bigtriangleup p}^{T}\mathbf{J}_{k}^{T}\Omega_{k}\mathbf{e}_{k}+\mathbf{\bigtriangleup p}^{T}\mathbf{J}_{k}^{T}\Omega_{k}\mathbf{J}_{k}\mathbf{\bigtriangleup p}) \\ & = \underset{\mathbf{\bigtriangleup p} }{argmin} \sum (\underbrace{\mathbf{e}_{k}^{T}\Omega_{k}\mathbf{e}_{k}}_{常数项} +2\cdot \mathbf{\bigtriangleup p}^{T}\mathbf{J}_{k}^{T}\Omega_{k}\mathbf{e}_{k}+\mathbf{\bigtriangleup p}^{T}\mathbf{J}_{k}^{T}\Omega_{k}\mathbf{J}_{k}\mathbf{\bigtriangleup p}) \\ & = \underset{\mathbf{\bigtriangleup p} }{argmin} \sum (2\cdot \mathbf{\bigtriangleup p}^{T}\mathbf{J}_{k}^{T}\Omega_{k}\mathbf{e}_{k}+\mathbf{\bigtriangleup p}^{T}\mathbf{J}_{k}^{T}\Omega_{k}\mathbf{J}_{k}\mathbf{\bigtriangleup p}) \\ & = \underset{\mathbf{\bigtriangleup p} }{argmin} [2 \mathbf{\bigtriangleup p}^{T}\cdot \sum \mathbf{J}_{k}^{T}\Omega_{k}\mathbf{e}_{k}+\mathbf{\bigtriangleup p}^{T}\cdot \sum \mathbf{J}_{k}^{T}\Omega_{k}\mathbf{J}_{k} \cdot \mathbf{\bigtriangleup p})] \\ \end{align}\]

其中，博主为了简化表示，将$\mathbf{e}_{k}(\mathbf{p})$简化为$\mathbf{e}_{k}$，得到的公式（9）非常重要，它表明，该目标优化问题是一个关于$\Delta\mathbf{p}$的二次型问题！这个发现很重要，决定了优化求解的稳定性。

接下来，这里我们计算公式（9）中的目标函数关于$\Delta \mathbf{p}$的导数，可以得到

\[\begin{matrix}& [2 \mathbf{\bigtriangleup p}^{T}\cdot \sum \mathbf{J}_{k}^{T}\Omega_{k}\mathbf{e}_{k}+\mathbf{\bigtriangleup p}^{T}\cdot \sum \mathbf{J}_{k}^{T}\Omega_{k}\mathbf{J}_{k} \cdot \mathbf{\bigtriangleup p})]^{\prime } \\ \\ & = 2\sum \mathbf{J}_{k}^{T}\Omega_{k}\mathbf{e}_{k} +2\sum \mathbf{J}_{k}^{T}\Omega_{k}\mathbf{J}_{k} \cdot \mathbf{\bigtriangleup p}\end{matrix}\]

令其导数$2\sum \mathbf{J}_{k}^{T}\Omega_{k}\mathbf{e}_{k} +2\sum \mathbf{J}_{k}^{T}\Omega_{k}\mathbf{J}_{k} \cdot \mathbf{\bigtriangleup p} = 0$，我们可以得到

\[2\sum \mathbf{J}_{k}^{T}\Omega_{k}\mathbf{J}_{k} \cdot \mathbf{\bigtriangleup p} + 2\sum \mathbf{J}_{k}^{T}\Omega_{k}\mathbf{e}_{k} = 0\]

可能你还觉得不够面熟，我们找个符号代替一下：

\[\begin{matrix} & \mathbf{H}\mathbf{\bigtriangleup p}-\mathbf{g} = \mathbf{0} \quad （GN中的增量方程） \\ where,\\ & \mathbf{H} = \sum \mathbf{J}_{k}^{T}\Omega_{k}\mathbf{J}_{k},\\\\ & \mathbf{g} = -\sum \mathbf{J}_{k}^{T}\Omega_{k}\mathbf{e}_{k}\end{matrix}\]

这样就熟悉多了，这不就是在线性代数课上学的线性方程求解问题么。没错是的，我们通过化简最终将优化问题转化为一个求解线性方程的问题，怎么求解，这个就不用多说了。这里的$\mathbf{H}$，通常被称为海森矩阵（Hessian Matrix），而且海森矩阵$\mathbf{H}$要求必须是正定矩阵，上述的化简才是有意义的，为啥嘞？我们能够看到这个线性方程的导数就是$\mathbf{H}$（目标函数的二阶导数），我们知道只有当一阶导数为0，二阶导数＞0时（$\mathbf{H}$为正定矩阵），我们求出来的才是严格意义上的最小值点。当然这只是一次迭代所求解的变换$\Delta \mathbf{T}$，多次迭代收敛后，我们就可以得到完整的刚性变换$\mathbf{T} = \prod \Delta \mathbf{T}$。

综上所述，给读者朋友们找了（实则网上扒 😏）一个简单的算法流程：

GN算法的基本流程

3. 列文伯格-马夸尔特优化算法（Levenberg-Marquadt，LM）

我们在第2章逐步推导了GN算法，并且我们得到了其精髓：

优化问题的求解——>线性方程组的求解问题
海森矩阵的近似：$\mathbf{H} = \sum \mathbf{J}_{k}^{T}\Omega_{k}\mathbf{J}_{k}$，即二阶导数可以用一阶导数近似

不难看出， GN算法通过在$\mathbf{p}$附近进行一阶泰勒展开来简化计算，但这有个前提，那就是$\Delta \mathbf{p}$不能太大，否则近似效果很差（因为$\mathbf{H}$不一定总是正定的，有可能是半正定的）。用数学的语言来说，$\Delta \mathbf{p}$是有一个置信区间的，只有在这个区间里面，我们才能信任它。这就给求解线性方程带来了很大的困扰，本来想着这个变换步长简单易求，但没想到这个步长长度不好把握，步长太短则老太太裹脚，步长太长则小鹿乱撞。

于是人们对GN算法作了进一步修正。所用的技巧是把一个绝对正定对角矩阵加到$\mathbf{H}$上去，改变原矩阵的特征值结构，使其变成较好的对称正定矩阵。因此LM中的增量方程为：

\[(\mathbf{H} +\lambda \mathbf{I} )\Delta p = \mathbf{g} \quad （LM中的增量方程）\]

其中，$\lambda$是一个正实数$\lambda > 0$，$\mathbf{I}$是一个单位矩阵。哎？这么一操作，发现了一些有趣的事情：

当$\lambda = 0$ 时，那LM算法就变成了GN算法了
当$\lambda \to \infty$时，我们把$\Delta \mathbf{p}$显式写出来，可以看到LM算法就变成了梯度下降法
当 $0< \lambda < \infty$时，LM算法的迭代步长介于GN算法与梯度下降法之间。

这样我们可以看出LM优化通过在增量方程中增加一个拉格朗日乘子$\lambda$来改善GN方法，避免由于$\Delta \mathbf{p}$过大，优化解质量不稳定的问题。在一次迭代中， $\mathbf{H}$和$\mathbf{g}$是不变的，如果我们发觉解出的$\Delta \mathbf{p}$过大，就适当调大$\lambda$，并重新计算增量方程，以获得相对小一些的$\Delta \mathbf{p}$；反过来，如果发觉解出的$\Delta \mathbf{p}$在合理的范围内，则适当减小$\lambda$，减小后的$\lambda$将用于下次迭代，相当于允许下次迭代时$\Delta \mathbf{p}$有更大的取值，以尽可能地加快收敛速度。通过这样的调控，LM算法即保证了收敛的稳定性，又加快了收敛速度。一切都很nice！

不过还有一个问题，我们如何判断$\Delta \mathbf{p}$是否是合理的呢？

我们可以定义一个总体的loss，来判断$\Delta \mathbf{p}$的好坏，对于公式（3）这样一个优化问题来说，一般$loss = \sum \mathbf{d}_{ij}$，我们优化的目标当然是让loss最小。如果加上$\Delta \mathbf{p}$后loss反而增大了，就证明$\Delta \mathbf{p}$超出了置信区间，我们需要调大$\lambda$，重新计算增量$\Delta \mathbf{p}$；如果loss变小，证明$\Delta \mathbf{p}$在合理区间内，调小$\lambda$，算法继续。

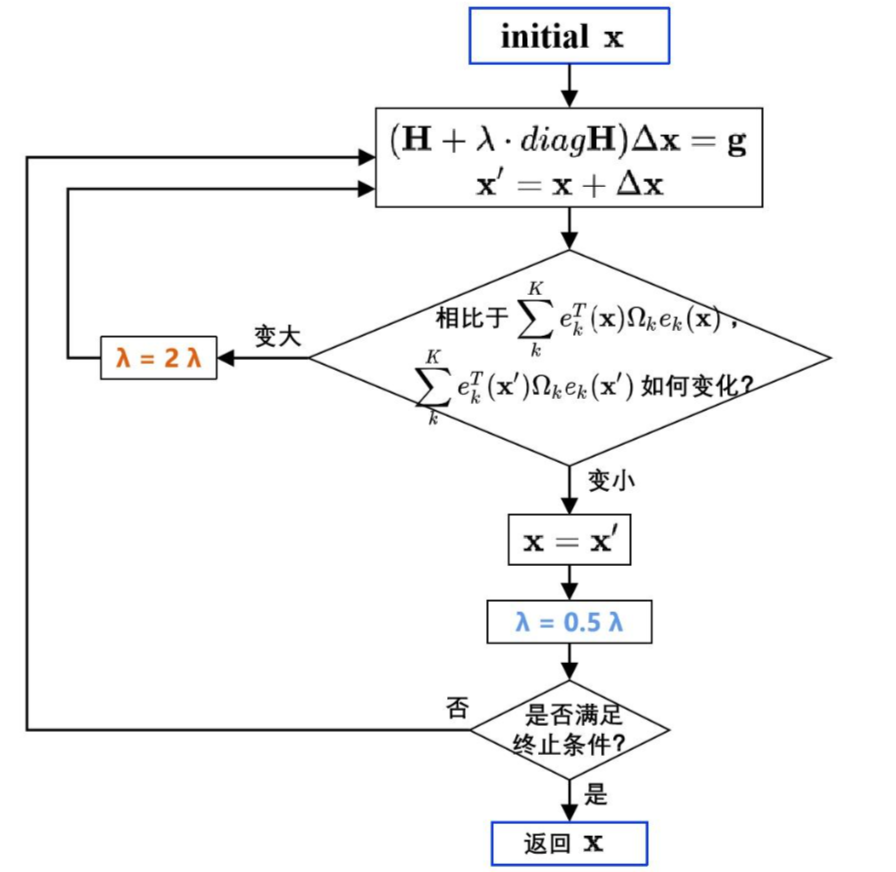
综上所述，LM算法的流程如下: